This is heart breaking anguish to read and post. I cannot stop thinking of the frac quake damages underground (of course not visible) and how much gas is migrating to surface, into and around the Simlik home. Is the gas sour? There are acid gas injection sites nearby so lots of sour gas – Farmington has been transformed into a frac’d hell hole.
Is there an explosive risk? Is deadly cancer-causing radon increasing with the fracs into and accumulating in the home? What frac chemicals are migrating to surface and into the home? Is the water contaminated? What toxic chemical brew is the Simlik family, and their livestock and pets breathing every day and night? What are the stress and health impacts from the incessant noise, traffic, dust, vibrations and light invasion compounding cumulatively with watching ones home disintegrate? Where is the “regulator?”
No wonder Earthquakes Canada is censoring frac quakes! What are the authorities hiding?
***
Hi Jessica
I’m sending you photos to illustrate what we’re dealing with here at our place in Farmington BC.
Our land is moving. The land didn’t heave and sink and slide around for the first 20 years we lived here. Because of the oil & gas industry’s addiction to the continued build out of excessive infrastructure which includes: pile driving, ground vibration, heavy equipment operating, gas plant operations, drilling, fracking, completions, injections and earthquakes, the ground never rests!
There is NO “oil & gas free zone” to move to in this area!
BC Ministry of Energy, Mines & Petroleum is offering for development – 2 sections of land RIGHT ACROSS the road from us. Considering the problems we’re already having, this is a bad idea.
Vicky Living-in-the-middle-of-a-gasfield Simlik
Quake Damages Photo A: The floor tiles are sliding out of alignment:

Quake Damages Photo B: Patio stones are lifting (similar damages experienced by Ann Craft from frac’ing by Quicksilver near Ponoka):

Quake C Photo: Siding on the house is buckling:

Quake D Photo: Interior home walls cracked and door ruined. No point repairing anything because the quakes keep undoing the repairs:

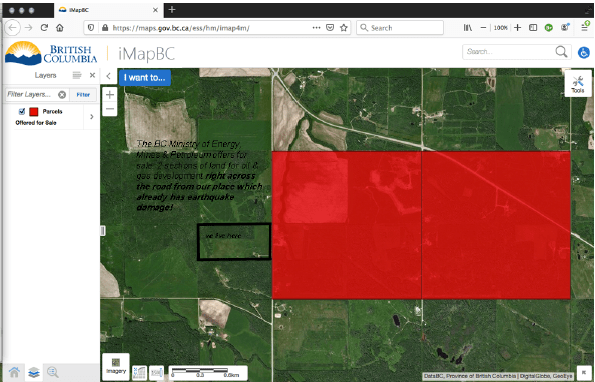
Quake E Photo: BC Ministry Energy & Mines offering for sale two sections of land for oil & gas development across the road from our already frac quake damaged property and home (red shows parcels for sale by BC; black box shows where we live):
Refer also to:
2020 01 16: Alberta: AGS confirms frac’ing caused 4.18M earthquake that rattled many homes from Sylvan Lake to Red Deer last March, knocked out power to 4,600 customers, and caused subsequent 3.13M and smaller cluster of quakes. “Complaints of damage from the event were received.” And a water well was damaged by frac’ing near Sylvan.
List of gas plants with SO2 emissions in NEBC, they dot the area like measles. Note the size of the emissions in the top three, thousands of tonnes of SO2 per year:

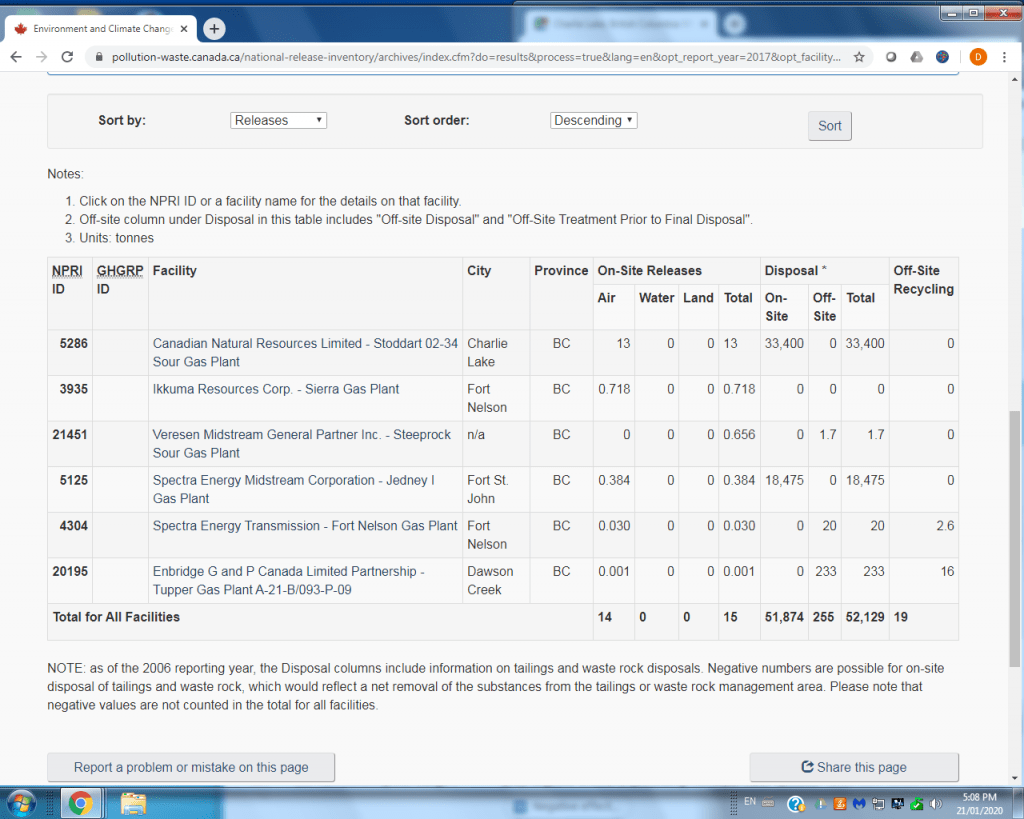
H2S emissions and disposal in NEBC – huge amounts of acid gas are being injected at Charlie Lake and Fort St. John, in tonnes:
In a single recent five-year span there were 73 documented sour gas leaks in B.C. and 34 workers died as a result of sour gas exposure since 1983.

Yellow dots are sour gas wells; red dots are schools in Dawson Creek/Fort St. John area.
“Who wants to live close to a gas plant or wells that [could leak] dangerous H2S?”
Living in the middle of a gas field in Canada
